
Prova e exemplos do teorema binomial
O teorema binomial é uma equação que nos diz como desenvolver uma expressão da forma (a + b)n para algum número natural n. Um binômio nada mais é do que a soma de dois elementos, como (a + b). Também nos permite saber para um termo dado por umkbn-k qual é o coeficiente que o acompanha.
Este teorema é comumente atribuído ao inventor, físico e matemático inglês Sir Isaac Newton; No entanto, foram encontrados vários registros que indicam que sua existência já era conhecida no Oriente Médio, por volta do ano 1000.

Índice do artigo
- 1 números combinatórios
- 2 demo
- 3 exemplos
- 3.1 Identidade 1
- 3.2 Identidade 2
- 4 Outra demonstração
- 4.1 Prova por indução
- 5 curiosidades
- 6 referências
Números combinatórios
O teorema binomial nos diz matematicamente o seguinte:
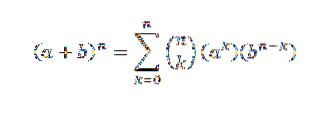
Nesta expressão, aeb são números reais en é um número natural.
Antes de fazer a demonstração, vamos dar uma olhada em alguns conceitos básicos que são necessários.
O número combinatório ou combinações de n em k são expressos da seguinte forma:
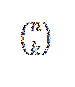
Esta forma expressa o valor de quantos subconjuntos com k elementos podem ser escolhidos de um conjunto de n elementos. Sua expressão algébrica é dada por:
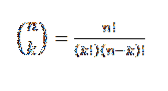
Vejamos um exemplo: suponha que temos um grupo de sete bolas, das quais duas são vermelhas e as demais são azuis..
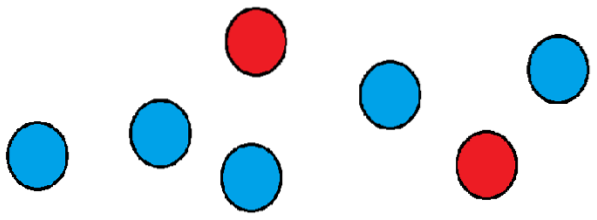
Queremos saber de quantas maneiras podemos organizá-los em uma fileira. Uma forma poderia ser colocar as duas vermelhas na primeira e segunda posições, e o resto das bolas nas posições restantes..
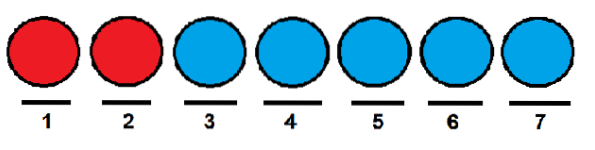
Semelhante ao caso anterior, poderíamos dar às bolas vermelhas a primeira e a última posição, respectivamente, e ocupar as outras com bolas azuis.
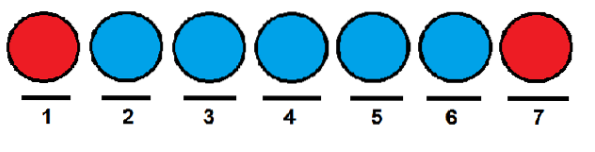
Agora, uma maneira eficiente de contar quantas maneiras podemos organizar as bolas em uma linha é usando números combinatórios. Podemos ver cada posição como um elemento do seguinte conjunto:
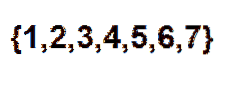
Então, resta escolher um subconjunto de dois elementos, em que cada um desses elementos representa a posição que as bolas vermelhas irão ocupar. Podemos fazer essa escolha de acordo com a relação dada por:
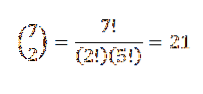
Desta forma, temos que existem 21 maneiras de ordenar essas bolas.
A ideia geral deste exemplo será muito útil para provar o teorema binomial. Vejamos um caso particular: se n = 4, temos (a + b)4, que nada mais é do que:
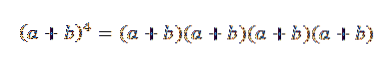
Ao desenvolver este produto, ficamos com a soma dos termos obtidos pela multiplicação de um elemento de cada um dos quatro fatores (a + b). Assim, teremos termos que serão da forma:
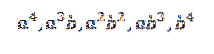
Se quiséssemos obter o termo do formulário a4, basta multiplicar da seguinte forma:
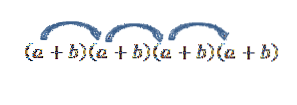
Observe que só existe uma maneira de obter esse elemento; mas, o que acontece se procurarmos agora o termo da forma adoisbdois? Como “a” e “b” são números reais e, portanto, a lei comutativa é válida, temos que uma forma de obter este termo é multiplicar pelos membros indicados pelas setas.
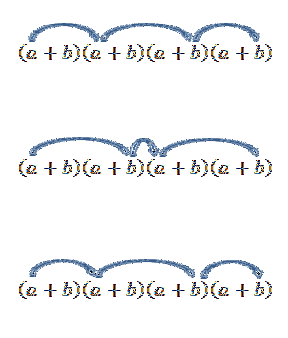
Realizar todas essas operações é geralmente um tanto tedioso, mas se virmos o termo "a" como uma combinação em que queremos saber de quantas maneiras podemos escolher dois "a" de um conjunto de quatro fatores, podemos usar a ideia do exemplo anterior. Portanto, temos o seguinte:
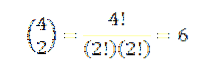
Assim, sabemos que na expansão final da expressão (a + b)4 teremos exatamente 6adoisbdois. Usando a mesma ideia para os outros elementos, você deve:
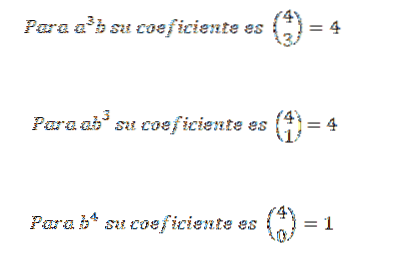
Em seguida, adicionamos as expressões obtidas anteriormente e temos isso:
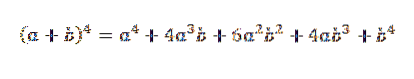
É uma prova formal para o caso geral em que "n" é qualquer número natural.
Demonstração
Observe que os termos que permanecem durante o desenvolvimento (a + b)n Eles são da forma dekbn-k, onde k = 0,1,…, n. Usando a ideia do exemplo anterior, temos a maneira de escolher as variáveis "k" "a" dos fatores "n":
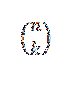
Ao escolher desta forma, estamos escolhendo automaticamente n-k variáveis "b". Disto se segue que:
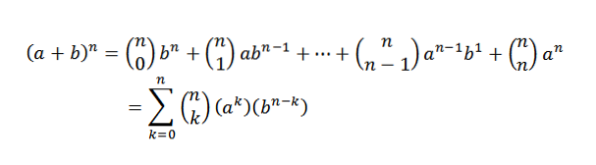
Exemplos
Considerando (a + b)5, Qual seria o seu desenvolvimento?
Pelo teorema binomial, temos:
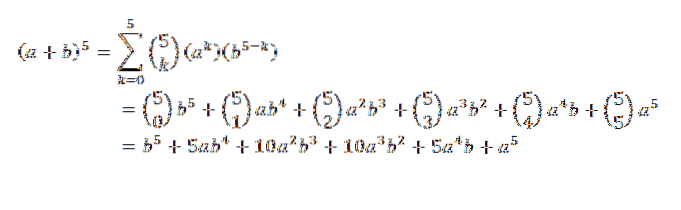
O teorema binomial é muito útil se temos uma expressão na qual queremos saber qual é o coeficiente de um termo específico sem ter que fazer a expansão completa. Como exemplo, podemos tomar a seguinte incógnita: qual é o coeficiente de x7Y9 na expansão de (x + y)16?
Pelo teorema binomial, temos que o coeficiente é:
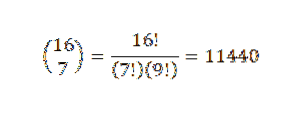
Outro exemplo seria: qual é o coeficiente de x5Y8 no desenvolvimento de (3x-7y)13?
Primeiro, reescrevemos a expressão de uma maneira conveniente; isto é:
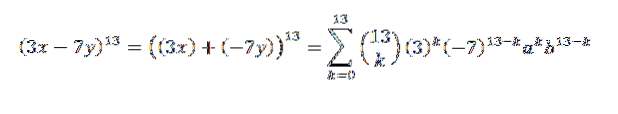
Então, usando o teorema binomial, temos que o coeficiente buscado é quando temos k = 5
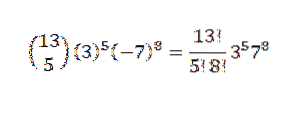
Outro exemplo dos usos deste teorema está na prova de algumas identidades comuns, como as que mencionaremos a seguir..
Identidade 1
Se "n" é um número natural, temos:
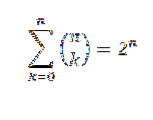
Para a prova usamos o teorema binomial, onde "a" e "b" tomam o valor de 1. Então temos:
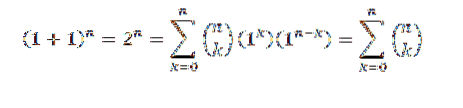
Desta forma, provamos a primeira identidade.
Identidade 2
Se "n" é um número natural, então
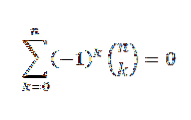
Pelo teorema binomial, temos:
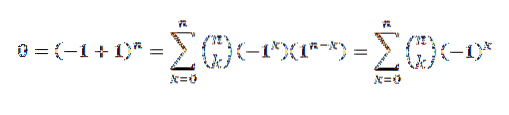
Outra demonstração
Podemos fazer uma prova diferente para o teorema binomial usando o método indutivo e a identidade de Pascal, que nos diz que, se “n” e “k” são inteiros positivos que satisfazem n ≥ k, então:
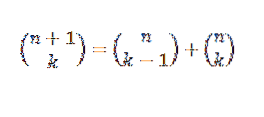
Prova de indução
Primeiro, vamos ver se a base indutiva se mantém. Se n = 1, temos:
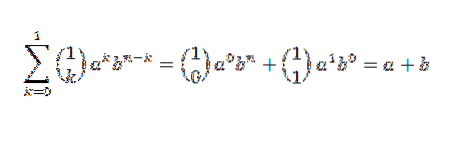
Na verdade, vemos que isso é cumprido. Agora, seja n = j tal que:
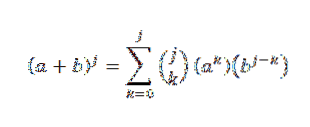
Queremos ver que para n = j + 1 é verdade que:
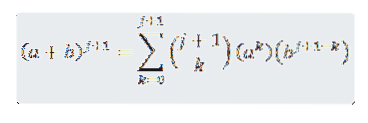
Portanto, temos que:
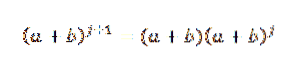
Por hipótese, sabemos que:
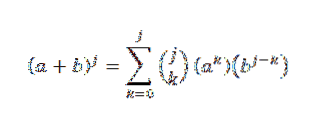
Então, usando a propriedade distributiva:
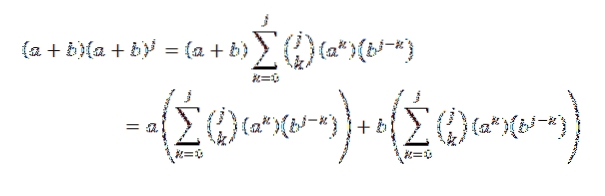
Posteriormente, desenvolvendo cada uma das somas, temos:
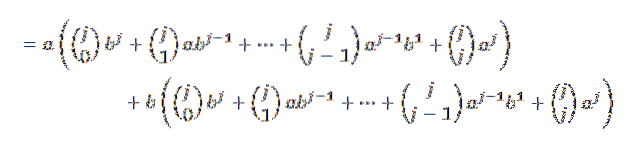
Agora, se agruparmos de uma forma conveniente, temos que:
Usando a identidade de pascal, temos:
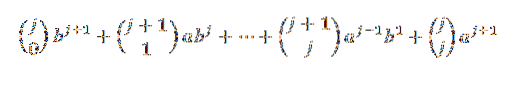
Finalmente, observe que:
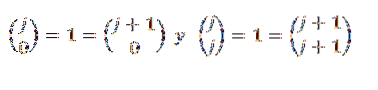
Portanto, vemos que o teorema binomial é válido para todos os "n" pertencentes aos números naturais, e com isso a prova termina.
Curiosidades
O número combinatório (nk) também é chamado de coeficiente binomial porque é precisamente o coeficiente que aparece no desenvolvimento do binomial (a + b)n.
Isaac Newton deu uma generalização deste teorema para o caso em que o expoente é um número real; este teorema é conhecido como teorema binomial de Newton.
Já nos tempos antigos, esse resultado era conhecido para o caso particular em que n = 2. Este caso é mencionado no Elementos por Euclides.
Referências
- Johnsonbaugh Richard. Matemática discreta. PHH
- Kenneth.H. Rosen, Discrete Mathematics and its Applications. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Seymour Lipschutz Ph.D e Marc Lipson. Discrete Mathematics. McGRAW-HILL.
- Ralph P. Grimaldi. Matemática Discreta e Combinatória. Addison-Wesley Iberoamericana
- Verde Star Luis… Matemática Discreta e Combinatória.Anthropos



Ainda sem comentários