
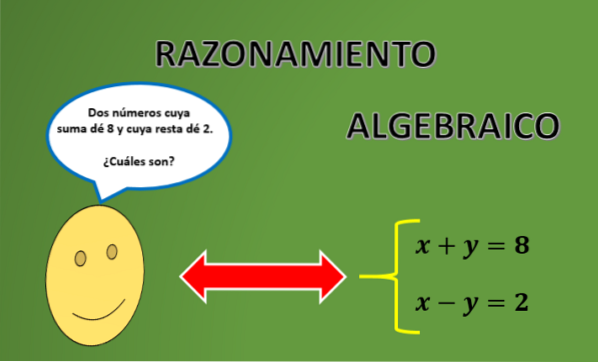
Raciocínio algébrico (com exercícios resolvidos)
O raciocínio algébrico Consiste essencialmente em comunicar um argumento matemático através de uma linguagem especial, que o torna mais rigoroso e geral, valendo-se de variáveis algébricas e operações definidas entre si. Uma característica da matemática é o rigor lógico e a tendência abstrata usados em seus argumentos..
Para isso é necessário saber a "gramática" correta a ser usada nesta redação. Além disso, o raciocínio algébrico evita ambigüidades na justificativa de um argumento matemático, o que é essencial para provar qualquer resultado em matemática..
Índice do artigo
- 1 variáveis algébricas
- 2 expressões algébricas
- 2.1 Exemplos
- 3 exercícios resolvidos
- 3.1 Primeiro exercício
- 3.2 Segundo exercício
- 3.3 Terceiro exercício
- 4 referências
Variáveis algébricas
Uma variável algébrica é simplesmente uma variável (uma letra ou símbolo) que representa um certo objeto matemático..
Por exemplo, as letras x, y, z são freqüentemente usadas para representar os números que satisfazem uma determinada equação; as letras p, q r, para representar fórmulas proposicionais (ou suas respectivas letras maiúsculas para representar proposições específicas); e as letras A, B, X, etc., para representar conjuntos.
O termo "variável" enfatiza que o objeto em questão não é fixo, mas varia. É o caso de uma equação, em que variáveis são utilizadas para determinar soluções que, em princípio, são desconhecidas..
Em termos gerais, uma variável algébrica pode ser considerada como uma letra que representa algum objeto, seja ele fixo ou não..
Assim como as variáveis algébricas são usadas para representar objetos matemáticos, também podemos considerar símbolos para representar operações matemáticas.
Por exemplo, o símbolo "+" representa a operação "adição". Outros exemplos são as diferentes notações simbólicas de conectivos lógicos no caso de proposições e conjuntos..
Expressões algébricas
Uma expressão algébrica é uma combinação de variáveis algébricas por meio de operações previamente definidas. Exemplos disso são as operações básicas de adição, subtração, multiplicação e divisão entre números, ou os conectivos lógicos em proposições e conjuntos..
O raciocínio algébrico é responsável por expressar um raciocínio ou argumento matemático por meio de expressões algébricas.
Essa forma de expressão ajuda a simplificar e abreviar a escrita, pois faz uso de notações simbólicas e permite uma melhor compreensão do raciocínio, apresentando-o de forma mais clara e precisa..
Exemplos
Vejamos alguns exemplos que mostram como o raciocínio algébrico é usado. É usado muito regularmente para resolver problemas de lógica e raciocínio, como veremos em breve..
Considere a conhecida proposição matemática "a soma de dois números é comutativa". Vamos ver como podemos expressar essa proposição algebricamente: dados dois números "a" e "b", o que essa proposição significa é que a + b = b + a.
O raciocínio usado para interpretar a proposição inicial e expressá-la em termos algébricos é o raciocínio algébrico..
Também poderíamos citar a famosa expressão "a ordem dos fatores não altera o produto", que se refere ao fato de que o produto de dois números também é comutativo, e algebricamente é expresso como axb = bxa.
Da mesma forma, as propriedades associativas e distributivas para adição e produto, nas quais a subtração e a divisão estão incluídas, podem ser (e de fato são) expressas algebricamente..
Esse tipo de raciocínio abrange uma linguagem muito ampla e é usado em muitos contextos diferentes. Dependendo de cada caso, nestes contextos é necessário reconhecer padrões, interpretar frases e generalizar e formalizar a sua expressão em termos algébricos, proporcionando um raciocínio válido e sequencial..
Exercícios resolvidos
A seguir estão alguns problemas de lógica, que vamos resolver usando o raciocínio algébrico:
Primeiro exercício
Qual é o número que, pegando metade dele, é igual a um?
Solução
Para resolver este tipo de exercício, é muito útil representar o valor que queremos determinar por meio de uma variável. Nesse caso, queremos encontrar um número que, pegando metade dele, forneça o número um como resultado. Vamos denotar por x o número procurado.
"Tirar a metade" de um número implica dividi-lo por 2. Portanto, o acima pode ser expresso algebricamente como x / 2 = 1, e o problema se resume em resolver uma equação, que neste caso é linear e muito fácil de resolver. Resolvendo para x, obtemos que a solução é x = 2.
Em conclusão, 2 é o número que ao tirar a metade é igual a 1.
Segundo exercício
Quantos minutos até a meia-noite se há 10 minutos 5/3 do que resta agora?
Solução
Denotemos por "z" o número de minutos até a meia-noite (qualquer outra letra pode ser usada). Em outras palavras, agora temos “z” minutos até a meia-noite. Isso implica que há 10 minutos faltavam “z + 10” minutos para chegar à meia-noite, e isso corresponde a 5/3 do que falta agora; ou seja, (5/3) z.
Então, o problema se resume em resolver a equação z + 10 = (5/3) z. Multiplicando ambos os lados da igualdade por 3, obtemos a equação 3z + 30 = 5z.
Agora, ao agrupar a variável "z" em um lado da igualdade, obtemos que 2z = 15, o que implica que z = 15.
Então faltam 15 minutos para a meia-noite.
Terceiro exercício
Em uma tribo que pratica a troca, existem estas equivalências:
- Uma lança e um colar são trocados por um escudo.
- Uma lança é equivalente a uma faca e um colar.
- Dois escudos são trocados por três unidades de facas.
Quantos colares uma lança é equivalente a?
Solução
Sean:
Co = um colar
L = uma lança
E = um escudo
Cu = uma faca
Portanto, temos os seguintes relacionamentos:
Co + L = E
L = Co + Cu
2E = 3Cu
Portanto, o problema se resume em resolver um sistema de equações. Apesar de ter mais incógnitas do que equações, este sistema pode ser resolvido, pois não nos pedem uma solução específica, mas sim uma das variáveis em função da outra. O que devemos fazer é expressar "Co" em termos de "L" exclusivamente.
Da segunda equação temos que Cu = L - Co. Substituindo na terceira obtemos que E = (3L - 3Co) / 2. Finalmente, substituindo na primeira equação e simplificando obtém-se que 5Co = L; ou seja, uma lança é igual a cinco colares.
Referências
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matemática: uma abordagem de solução de problemas para professores do ensino fundamental. Editores López Mateos.
- Fuentes, A. (2016). MATEMÁTICA BÁSICA. Uma introdução ao cálculo. Lulu.com.
- García Rua, J., & Martínez Sánchez, J. M. (1997). Matemática básica elementar. Ministério da Educação.
- Rees, P. K. (1986). Álgebra. Reverter.
- Rock, N. M. (2006). Álgebra I é fácil! Tão fácil. Team Rock Press.
- Smith, S. A. (2000). Álgebra. Pearson Education.
- Szecsei, D. (2006). Matemática Básica e Pré-Álgebra (edição ilustrada). Imprensa de carreira.


Ainda sem comentários