Aplicativos de decomposição aditiva, partições, gráficos

O decomposição aditiva de um número inteiro positivo é expressá-lo como uma soma de dois ou mais números inteiros positivos. Assim, temos que o número 5 pode ser expresso como 5 = 1 + 4, 5 = 2 + 3 ou 5 = 1 + 2 + 2. Cada uma dessas maneiras de escrever o número 5 é o que chamaremos de decomposição aditiva.

Se prestarmos atenção, podemos ver que as expressões 5 = 2 + 3 e 5 = 3 + 2 representam a mesma composição; ambos têm os mesmos números. No entanto, apenas por conveniência, cada um dos adendos é geralmente escrito seguindo o critério do menor ao maior.

Índice do artigo

• 1 decomposição aditiva
• 2 Decomposição aditiva canônica
• 3 aplicativos
  • 3.1 Teorema do exemplo
• 4 partições
  • 4.1 Definição
• 5 gráficos
• 6 referências

Decomposição aditiva

Como outro exemplo, podemos pegar o número 27, que podemos expressar como:

27 = 7 + 10 + 10

27 = 9 + 9 + 9

27 = 3 + 6 + 9 + 9

27 = 9 + 18

A decomposição aditiva é uma ferramenta muito útil que nos permite reforçar nosso conhecimento de sistemas de numeração.

Decomposição aditiva canônica

Quando temos números com mais de dois dígitos, uma maneira particular de decompô-los é nos múltiplos de 10, 100, 1000, 10.000, etc., que os compõem. Essa forma de escrever qualquer número é chamada de decomposição aditiva canônica. Por exemplo, o número 1456 pode ser decomposto da seguinte forma:

1456 = 1000 + 400+ 50 + 6

Se tivermos o número 20 846 295, sua decomposição aditiva canônica será:

20 846 295 = 20.000.000 + 800.000 + 40.000 + 6.000 + 200 + 90 +5.

Graças a esta decomposição, podemos ver que o valor de um determinado dígito é dado pela posição que ocupa. Vamos pegar os números 24 e 42 como exemplo:

24 = 20 + 4

42 = 40 +2

Aqui podemos ver que em 24 o 2 tem um valor de 20 unidades e o 4 um valor de 4 unidades; por outro lado, em 42, o 4 tem um valor de 40 unidades e o 2 de duas unidades. Assim, embora ambos os números usem os mesmos dígitos, seus valores são totalmente diferentes devido à posição que ocupam.

Formulários

Uma das aplicações que podemos dar à decomposição aditiva é em certos tipos de provas, nas quais é muito útil ver um inteiro positivo como a soma de outros.

Teorema do exemplo

Tomemos como exemplo o seguinte teorema com suas respectivas provas.

- Seja Z um número inteiro de 4 dígitos, então Z é divisível por 5 se seu número de unidades for zero ou cinco.

Demonstração

Vamos lembrar o que é divisibilidade. Se tivermos inteiros “a” e “b”, dizemos que “a” divide “b” se houver um inteiro “c” tal que b = a * c.

Uma das propriedades de divisibilidade nos diz que se “a” e “b” são divisíveis por “c”, então a subtração “a-b” também é divisível..

Seja Z um número inteiro de 4 dígitos; portanto, podemos escrever Z como Z = ABCD.

Usando a decomposição aditiva canônica, temos:

Z = A * 1000 + B * 100 + C * 10 + D

É claro que A * 1000 + B * 100 + C * 10 é divisível por 5. Por esta razão, temos que Z é divisível por 5 se Z - (A * 1000 + B * 100 + C * 10) é divisível por 5.

Mas Z - (A * 1000 + B * 100 + C * 10) = D e D é um número de um único dígito, então a única maneira de ser divisível por 5 é ser 0 ou 5.

Portanto, Z é divisível por 5 se D = 0 ou D = 5.

Observe que se Z tem n dígitos a prova é exatamente a mesma, só muda que agora escreveríamos Z = A₁PARA_dois… PARA_n e o objetivo seria provar que A_n é zero ou cinco.

Partições

Dizemos que uma partição de um inteiro positivo é uma maneira pela qual podemos escrever um número como uma soma de inteiros positivos.

A diferença entre uma decomposição aditiva e uma partição é que, enquanto a primeira busca que pelo menos possa ser decomposta em dois adendos ou mais, a partição não possui esta restrição.

Assim nós temos o seguinte:

5 = 5

5 = 1 + 4

5 = 2 + 3

5 = 1 + 2 + 2

Acima são partições de 5.

Ou seja, temos que toda decomposição aditiva é uma partição, mas nem toda partição é necessariamente uma decomposição aditiva..

Na teoria dos números, o teorema fundamental da aritmética garante que cada inteiro pode ser escrito exclusivamente como um produto de números primos.

Ao estudar partições, o objetivo é determinar de quantas maneiras um inteiro positivo pode ser escrito como a soma de outros inteiros. Portanto, definimos a função de partição conforme apresentado abaixo.

Definição

A função de partição p (n) é definida como o número de maneiras que um inteiro positivo n pode ser escrito como uma soma de inteiros positivos.

Voltando ao exemplo de 5, temos que:

5 = 5

5 = 1 + 4

5 = 2 + 3

5 = 1 + 1 + 3

5 = 1 + 2 + 2

5 = 1 + 1 + 1 + 2

5 = 1 + 1 + 1 + 1 + 1

Assim, p (5) = 7.

Gráficos

Ambas as partições e decomposições aditivas de um número n podem ser representadas geometricamente. Suponha que temos uma decomposição aditiva de n. Nesta decomposição, os adendos podem ser arranjados de forma que os membros da soma sejam ordenados do menor para o maior. Então, ok:

n = a₁ + para_dois + para₃ +… + A_r com

para₁ ≤ a_dois ≤ a₃ ≤… ≤ a_r.

Podemos representar graficamente essa decomposição da seguinte maneira: em uma primeira linha marcamos o a₁-pontos, então no próximo marcamos_dois-pontos, e assim por diante até chegar a um_r.

Tome por exemplo o número 23 e sua seguinte decomposição:

23 = 5 + 4 + 7 + 3 + 1 +3

Ordenamos esta decomposição e temos:

23 = 1 + 3 + 3 + 4+ 5 + 7

Seu gráfico correspondente seria:

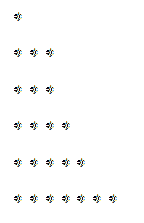
Da mesma forma, se lermos o referido gráfico verticalmente em vez de horizontalmente, podemos obter uma decomposição possivelmente diferente da anterior. No exemplo de 23, o seguinte se destaca:

Portanto, temos 23, também podemos escrever como:

23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.

Referências

1. G.H. Hardy e E. M. Wright. Uma introdução à teoria dos números. Oxford Clarendon Press.
2. Navarro C. Enciclopédia Didática 6. Editorial Santillana, S.A..
3. Navarro C.Link para o Math 6. Editorial Santillana, S.A..
4. Niven e Zuckerman. Introdução à teoria dos números. Limusa.
5. Avaliação VV.AA Critério da área de matemática: um modelo para o ensino fundamental. Wolters Kluwer Education.
6. Enciclopédia Didática 6.